タンパク質の位相決定法 タンパク質のX線結晶構造解析において，回折X線の位相を求めることは構造解析が成功するかどうかを決める重要な過程です．しかしタンパク質結晶の回折強度からだけでは，位相角を求めることはできません．この問題を解決するために従来から用いられてきた方法が，重原子同形置換法です．この方法では純粋にタンパク質だけからなる結晶以外に，水銀などの重原子をタンパク質に配位させた重原子誘導体結晶も同時に作成する必要があります．最近ではある特定の原子の異常散乱項を複数の波長のX線を用いて測定し，そのシグナルを利用して構造解析を行う多波長異常分散（MAD）法も頻繁に行われるようになってきました．この方法では，遺伝子工学の手法を用いてメチオニンの硫黄原子をセレンに置換したセレノメチオニン化タンパク質の結晶を用いる方法が主流となっています．また重原子同形置換法とは違い，鉄や亜鉛などの比較的原子量の小さな原子でも構造解析を行なうことが可能です．タンパク質の中には生体内で鉄などと結合しているものもあり，そのようなタンパク質の構造解析では威力を発揮します．

Mnを用いた多波長異常分散法の試み これまでにFeを用いたMAD法による構造解析は数多く行われていますが，Mnを用いたMAD法による構造解析例は報告されていません．MnのK殻吸収端は約1.896A（6.539keV）にあり，Feよりもさらに長波長の領域に存在します．この波長領域では，X線の吸収が大きく，回折強度の低下を引き起こしてしまうため，非常に強力なX線が必要となります．また，吸収による結晶へのダメージが大きいことや，そこから生じるシステマチックなエラーがデータ内に混入するため，解析は非常に困難なものとなります．しかし今日では，シンクロトロン放射光施設の発展はますます目覚しく，広範囲の波長領域で安定した高輝度のX線を得ることが可能となってきました．そして第3世代の放射光施設であるSPring-8においては，Mnの吸収端をカバーするビームラインが建設され，現在では構造解析可能な良質なデータ収集は十分に可能だと考えられます．このように本研究は，MAD法に利用される原子種の限界を拡張するという意義を持った研究です． Mn-MADデータの測定 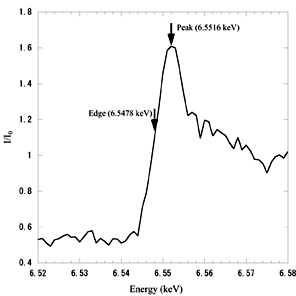MAD法においては，Bijvoet対での反射強度の差を最大限に利用するため，波長の選択を行う必要があります．よってあらかじめMnの吸収端付近でX線の吸収スペクトルを測定し， f”（異常分散シグナルの虚数項）が極大となる波長（Peak），および f’（異常分散シグナルの実数項）が極小となる波長（Edge）を決定します．実際に測定したMnのK殻吸収端付近での吸収スペクトルの結果を右上図に示した． Mn-MAD位相の計算 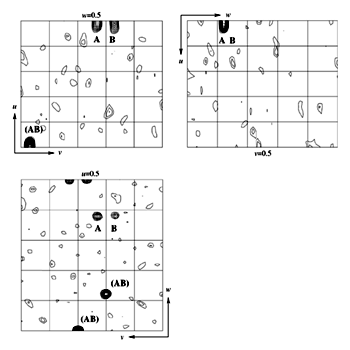タンパク質結晶構造解析における位相問題はパターソン関数を計算することで行います．重原子同形置換法では，ネイティブ結晶と誘導体結晶の反射強度の差を係数としたパターソン合成を行うことにより重原子のサイトを決定できます．MADデータの場合は，各波長のデータにおいてBijvoet対間のF″に起因する構造振幅の差（ΔFano）を係数とするパターソン合成（Bijvoet difference）と，波長間での構造振幅の差（ΔFiso）を係数とするパターソン合成 (Dispersive difference)を計算することができ，異常分散を引き起こす原子の原子間ベクトルを導きます．このベクトルを解釈することで，同形置換法と同様に異常分散原子のサイトを決定できます．右図にPeakのデータから計算したBijvoet差パターソン図のハーカー面（重原子のサイトに関係無く必ずピークが現れる面）を示しました．この図から，非対称単位中に2個のMnが存在することがはっきりと確認できました．このMnのサイトを利用して位相計算を行い，溶媒平滑化や分子平均化法の手法を用い位相の改良を行いました．その結果，2次構造を解釈できる程度のマップを計算することに成功しました．このマップをもとにポリアラニンモデルを部分的に構築し，プログラムSIGMAAおよびDMを用いた位相の組み合わせと改良を行い，全残基数の80%にあたるポリアラニンモデルを構築しました．最終的には，別の空間群に属する高分解能データを収集し，このポリアラニンモデルをサーチモデルとした分子置換法，および両結晶間での電子密度の平均化を行った結果，構造解析に成功しました．